Diese Seite funktioniert nur mit Javascript.
Die Grenzrate der Substitution2.2.5 Das HaushaltsoptimumKomparative Statik des Haushalts
Inzwischen besitzen wir zwei wichtige Informationen über die (Modell-)Haushalte: Wir wissen zum einen, was sie sich leisten können. Zum zweiten ist uns bekannt, was sie sich wünschen. Beides können wir grafisch darstellen: Was sie sich leisten können, bilden wir im Güterraum mit der Budgetrestriktion ab. Was sie sich wünschen, können wir im gleichen Diagramm mithilfe von Indifferenzkurven darstellen. Um zu sehen, wie sie sich ihre Wünsche unter der Budgetrestriktion bestmöglich erfüllen, müssen die beiden Aspekte nur noch zusammengeführt werden.
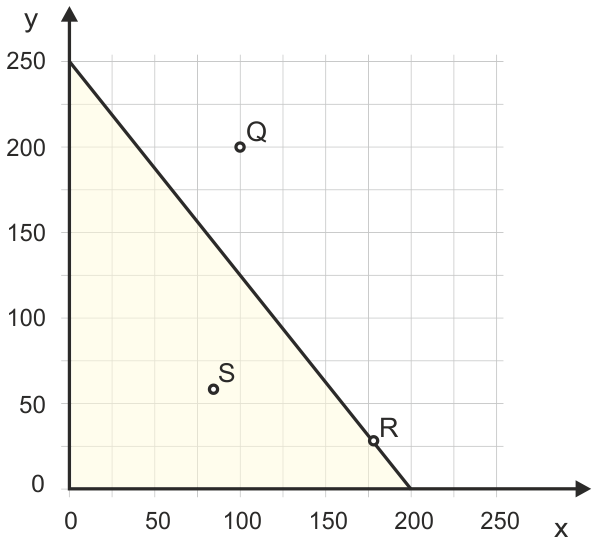
Dazu greifen wir das Zahlenbeispiel wieder auf, das wir bei der Konstruktion der Budgetgeraden eingesetzt haben. Der Haushalt kann mit einem Einkommen E in Höhe von 1000 Euro die Güter X und Y kaufen, die 5 bzw. 4 Euro pro Stück kosten. Die Budgetrestriktion, die wir ermittelt hatten, ist hier in Abbildung 1 noch einmal wiedergegeben. Das Güterbündel R könnte der Haushalt mit seinem Einkommen gerade bezahlen; S könnte er sich leisten, ohne sein Einkommen voll zu verausgaben, und zum Erwerb des Güterbündels Q würden die 1000 Euro Einkommen nicht ausreichen.
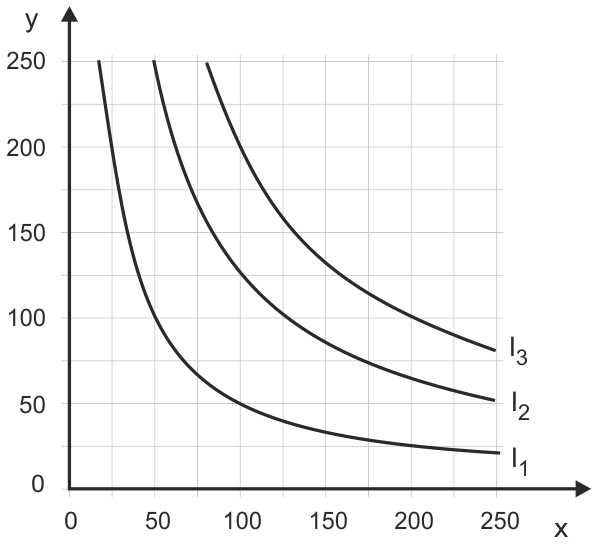
Wir wollen annehmen, dass der Haushalt über die Güter Präferenzen besitzt, die sich mithilfe der Nutzenfunktion $U = x \cdot y$ abbilden lassen. Dies ist die gleiche Nutzenfunktion, die wir im Käsebrötchen-Bier-Beispiel gefunden hatten und für die wir bereits Indifferenzkurven konstruiert haben. In Abbildung 2 sind drei ausgewählte Indifferenzkurven für diese Nutzenfunktion eingezeichnet. Die Indexwerte der Kurven in der maßstabsgetreuen Abbildung sind 5.000, 12.500 und 20.000.
Die Präferenzen des Haushalts hätten wir z.B. auch mit der Nutzenfunktion $U = \sqrt {x \cdot y} $ abbilden können. Hätten wir diese Funktion eingesetzt, hätten wir für die Nutzenindexwerte von 70,71, 111,80 und 141,42 eine identische Abbildung erhalten.
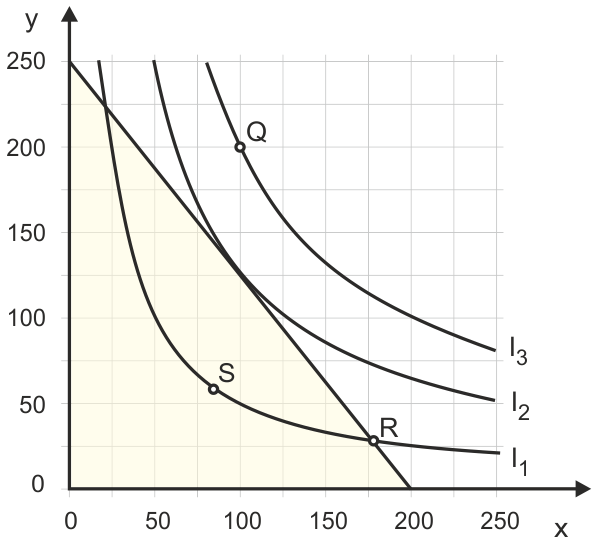
Nun bringen wir die beiden Gedanken, was der Haushalt möchte und was er sich leisten kann, zusammen, indem wir die beiden Diagramme aus Abbildung 1 und 2 einfach übereinander legen (s. Abb. 3). Die Indifferenzkurve I3 würde der Haushalt gerne erreichen (denn sie zeigt von den drei eingezeichneten Indifferenzkurven den höchsten Nutzen an), aber die Budgetrestriktion erlaubt es ihm nicht. Die höchste erreichbare Indifferenzkurve ist offenbar jene, die die Budgetgerade tangiert. Dabei stellt die Ausgewogenheitsannahme (Konvexität der Indifferenzkurven; abnehmende Grenzrate der Substitution) sicher, dass es einen eindeutigen Tangentialpunkt gibt.
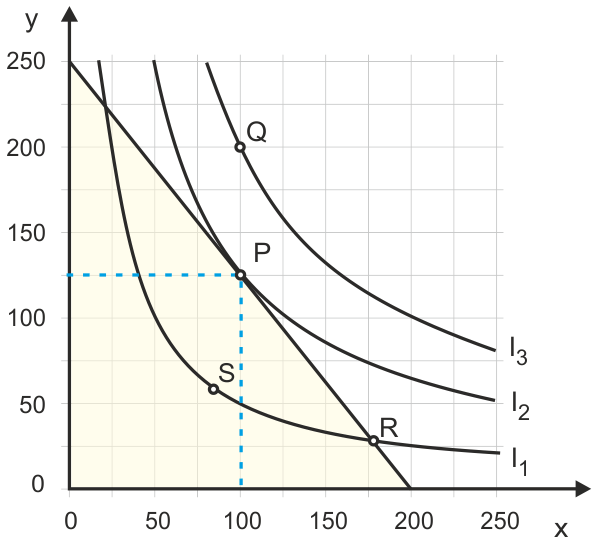
In Abbildung 4 ist der Tangentialpunkt gekennzeichnet. Der Haushalt erreicht den größtmöglichen Nutzen, wenn er sein Einkommen für das Güterbündel P ausgibt, also 100 X und 125 Y kauft - wie man aus der Grafik mit der "Methode des scharfen Hinsehens" ermitteln kann. Dieses Güterbündel bzw. der Punkt P heißt Haushaltsoptimum oder Haushaltsgleichgewicht.
Andernfalls wäre P kein Tangential-, sondern ein Schnittpunkt. Die (absolute) Steigung der Indifferenzkurve hatten wir im vorigen Abschnitt als Verhältnis der Grenznutzen von $x$ und $y$ ermittelt (s. dort Abb. 6 und Gleichung (5)). Die (absolute) Steigung der Budgetgeraden entspricht dem Preisverhältnis der Güter X und Y (s. Abb. 4). Also gilt im Haushaltsgleichgewicht, dass das Verhältnis der Grenznutzen der beiden Güter ihrem Preisverhältnis entspricht. Diese Aussage gilt auch für den n-Güter-Fall, so dass sich allgemein formulieren lässt:
Da das Grenznutzenverhältnis der negativen umgekehrten Grenzrate der Substitution entspricht, gilt auch:
Das sind ungewohnt klingende und schwer zu begreifende Aussagen. Aber ein Gegenbeispiel macht deutlich, dass es so sein muss. Dazu betrachten wir in Abbildung 5 einen Fall, in dem der Haushalt sich in Punkt R nicht im Gleichgewicht befindet. Das Verhältnis der Grenznutzen stimmt nicht mit dem Verhältnis der Güterpreise überein. Dieses beträgt 5/4 = 1,25 und zeigt mit einem negativen Vorzeichen die Steigung der Budgetgeraden. Also kann sich der Haushalt bei konstanten Ausgaben 1,25 Einheiten mehr von Gut Y leisten, wenn er auf eine Einheit von Gut X verzichtet.
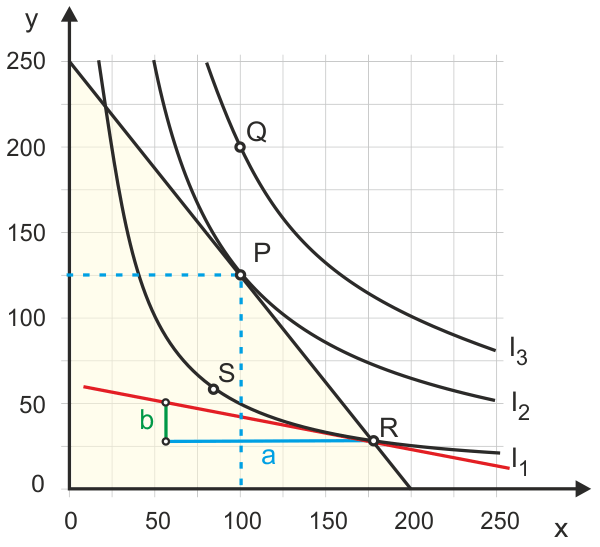
Nun ist in R eine Tangente angelegt, um erkennen zu können, in welchem Verhältnis der Haushalt die Güter bei Indifferenz gegeneinander tauschen würde. Die blaue Strecke a ist fast fünf mal so lang wie die grüne Strecke b. Also wäre der Haushalt bei Indifferenz bereit, für 1 Einheit von Gut Y 5 Einheiten von Gut X aufzugeben. Würde er tatsächlich 5 Einheiten X aufgeben, dann könnte er sich dafür 6,25 Einheiten Y kaufen. Bei den herrschenden Marktpreisen kann er also Y gegen X wesentlich günstiger eintauschen als es für Indifferenz notwendig wäre. Eine Einheit Y hätte ihm bereits für Indifferenz gereicht, tatsächlich erhält er 6,25 Einheiten. Konsequenterweise wird er sich auf der Budgetgerade nach oben bewegen, also mehr Y und weniger X konsumieren.
Wem ein Apfel zwei Birnen wert ist, der gibt sicher eine Birne her, wenn er dafür einen Apfel eintauschen kann. Das ist eine Selbstverständlichkeit. Aber es ist - so einfach es sich anhört - der Schlüssel zum Verstehen des Modells.
Während er nun von R in Richtung P "wandert", steigt der Konsum von Y und der von X nimmt ab. Das führt aufgrund des Gesetzes von der abnehmenden Grenzrate der Substitutiondazu, dass die Wertschätzung von Y abnimmt, während die Wertschätzung von X zunimmt. Bis der Haushalt den Punkt P erreicht, gilt aber im Prinzip immer die gleiche Überlegung wie im Punkt R: der Haushalt kann die Güter am Markt in einem besseren Verhältnis tauschen als notwendig, um seinen Nutzen konstant zu halten. Im Punkt P selbst kann er die Güter am Markt genau in dem Verhältnis tauschen, das seinen Nutzen konstant hält.
- Überprüfen Sie, ob Sie mit der Nutzenfunktion \( U = (xy)^{0,5}\) und der notwendigen Bedingung für ein Haushaltsgleichgewicht aus Gleichung (1) das gleiche Ergebnis erhalten wie im Zahlenbeispiel im nebenstehenden Text mit der Nutzenfunktion \( U = xy \).
-
Bevor Herr K. beschloss abzunehmen, war seine Nutzenfunktion \( U = 3S^{0,5}A^{0,5}\), wobei S für Schokolade und A für Äpfel steht. Der Preis für ein kg Schokolade beträgt \(p_S=4\), der Preis für ein kg Äpfel \(p_A=2\) Euro. Herr K. gibt jeden Monat 200 Euro für Äpfel und Schokolade aus.
Nach seinem Entschluss ist die Nutzenfunktion von Herrn K. \( U = 4S^{0,25}A\)
Wieviel kg Schokolade isst Herr K. weniger? -
Diskutieren Sie (und fertigen Sie dazu Skizzen an):
a) Wenn ein Haushalt im Optimum 21 Einheiten des Gutes X und 42 Einheiten des Gutes Y verbraucht, dann ist Gut X genau doppelt so teuer wie Gut Y.
b) Wenn sich das Einkommen des Haushalts verdreifacht, steigt der Konsum von x auf 63 und der von y auf 126 Einheiten.
Eine weitere Möglichkeit, sich darüber klar zu werden, warum es sich in Abb. 5 bei R nicht um das Optimum des Haushalts handeln kann, ist folgende: Wenn man auf der Indifferenzkurve von R aus in Richtung S wandert, bleibt der Nutzen konstant. Zugleich begibt man sich aber unter die Budgetgerade. Der Haushalt gibt sein Einkommen also nicht mehr wie in R voll aus. Das bedeutet doch offensichtlich, dass er "sich den gleichen Nutzen für weniger Geld kaufen kann". Dann kann er aber in R unmöglich in einer optimalen Situation gewesen sein. Den in P erreichten Nutzen hingegen kann der Haushalt nicht mit einem geringeren Betrag als seinem gesamten Einkommen "kaufen". Aus P heraus ist demnach keine Verbesserung möglich. Somit ist P optimal. (Diese Argumentation ist eng verbunden mit einer unter dem Stichwort "Duales Problem" bekannten Überlegung: Für das gegebene Nutzenniveau der Indifferenzkurve I2 wird bei gegeben Preisen die Konsumsumme (= das Einkommen) minimiert. Es wird also die geringstmögliche Ausgabe des Haushalts zur Erlangung dieses Nutzenniveaus gesucht. Auch auf diese Art und Weise stellt sich augenscheinlich P als Haushaltsgleichgewicht heraus - und der Augenschein trügt ausnahmsweise einmal nicht.)
Wer informiert ist, wie man $U\left( {x,y} \right)$ unter der Nebenbedingung $E = {p_x}x + {p_y}y$ maximiert, hätte die notwendige Bedingung für ein Haushaltsgleichgewicht auch berechnen können:
$$\left[ { - {{{\rm{d}}y} \over {{\rm{d}}x}} = } \right]\,\,\,\,{{\,\,\,{{\partial \,U} \over {\partial \,x}}\,\,\,} \over {{{\partial \,U} \over {\partial \,y}}}} = {{{p_x}} \over {{p_y}}} \tag{1}$$Für das Zahlenbeispiel mit der Nutzenfunktion $U=x \cdot y$ erhält man
$${y \over x} = {5 \over 4} \tag{2}$$und unter Ausnutzung der Gleichung der Budgetgerade $1000 = 5x + 4y$ die optimalen Mengen $y^* = 125$ und $x^* = 100$.
Das wesentliche Ergebnis dieses Abschnitts lautet in zwei Versionen:
Dieses Ergebnis ist auch als Zweites Gossensches Gesetz(synonym: Equimarginalprinzip, Grenznutzenausgleichsregel, Gesetz vom Ausgleich der gewogenen Grenznutzen, Gossensches Grenznutzenausgleichsgesetz) bekannt.
Das nächste Weihnachten kommt bestimmt ...
Überlegen Sie mithilfe des Konzepts des Haushaltsgleichgewichts, warum ein Geldgeschenk in der Regel (und unter den getroffenen Annahmen) mehr Freude bereitet als ein Sachgeschenk.
Geld schenken
Zur Beantwortung der Frage sei unterstellt, der zu beschenkende Haushalt befinde sich ausgangs in einem Gleichgewicht (Punkt P in Abbildung 1). Sein Einkommen betrage 600 Euro, die Preise für die Güter X und Y seien 4 Euro bzw. 3 Euro (schwarze Budgetgerade in Abbildung 1).
Der Schenker, der die Präferenzen (und somit die Indifferenzkurven) des Haushalts nicht kennt, macht dem Haushalt ein Geschenk im Wert von 100 Euro, indem er ihm 25 Stück des Gutes X schenkt. Dadurch erreicht der Haushalt Punkt R.
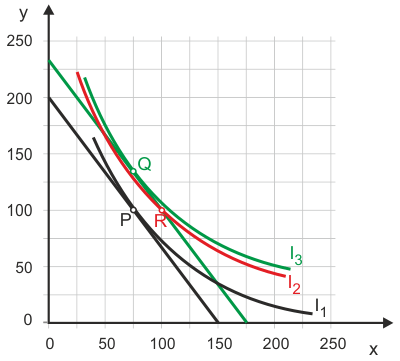
Mit gleich hoher Zunahme der Ausgaben erreicht der Haushalt in Q einen höheren Nutzen als in R.
Ein Problem
Wie immer blendet unsere Analyse natürlich einiges aus; z. B. die Schadenfreude des Beschenkten daran, dass den Schenker die Wahl und Besorgung des Geschenkes viel Zeit und Mühe gekostet hat. Vielleicht wäre ein Waffenstillstand die optimale Lösung: Ich schenke Dir nichts, solange Du mir nichts schenkst.
Das stiftet ihm fraglos Nutzen. Aber offensichtlich hätte der Haushalt eine höhere Indifferenzkurve erreichen können, wenn er das Geschenk im Wert von 100 Geldeinheiten nicht als Sach-, sondern als Geldgeschenk erhalten hätte. In diesem Fall hätte er sich nämlich für Punkt Q entschieden und die 100 Geldeinheiten vollständig für Gut y ausgegeben. Nur zufällig träfe der Schenker das optimale Geschenk, d. h. die Situtation, bei der die um den Wert des Geschenks verlagerte Budgetgerade eine Indifferenzkurve tangiert (wie hier in Punkt Q).
Die Fehleinschätzung der Präferenzen der Beschenkten durch die Schenker führt also zu einem Allokationsverlust. Wer nun meint, was soll's: Dieser Gedanke lässt sich nahtlos auf die Diskussion übertragen, ob man Bedürftige mit Geld- oder Sachleistungen unterstützen soll. Wer sich für Sachleistungen entscheidet, gibt indirekt zu erkennen, dass er überzeugt ist, besser zu wissen, was für die Bedürftigen gut ist, als diese selbst.
Und noch ein Problem
Macht Homo Oeconomicus anderen überhaupt Geschenke?
Fazit: Wenn der Schenker die Präferenzen des zu beschenkenden Haushalts nicht kennt, ist er mit einem Geldgeschenk auf der sicheren Seite. Denken Sie einmal darüber nach, wenn Sie das nächste mal ein Geschenk mit den Worten überreicht bekommen: "Ich habe den Kassenbon noch. Du kannst es ja umtauschen, wenn's Dir nicht gefällt."
Nach ähnlichen Seiten im WWW suchen